Answer:
1) increasing on (-∞,-1] ∪ [1,∞), decreasing on [-1,0) ∪ (0,1]
 is local maximum,
is local maximum,
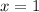 is local minimum
is local minimum
2) increasing on [1,∞), decreasing on (-∞,0) ∪ (0,1]
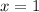 is absolute minimum
is absolute minimum
3) increasing on (-∞,0] ∪ [8,∞), decreasing on [0,4) ∪ (4,8]
 is local maximum,
is local maximum,
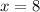 is local minimum
is local minimum
4) increasing on [2,∞), decreasing on (-∞,2]
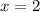 is absolute minimum
is absolute minimum
5) increasing on the interval (0,4/9], decreasing on the interval [4/9,∞)
 is local minimum,
is local minimum,
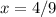 is absolute maximum
is absolute maximum
Explanation:
To find minima and maxima the of the function, we must take the derivative and equalize it to zero to find the roots.
1)
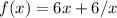
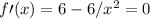 and
and
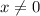
So, the roots are
 and
and
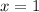
The function is increasing on the interval (-∞,-1] ∪ [1,∞)
The function is decreasing on the interval [-1,0) ∪ (0,1]
 is local maximum,
is local maximum,
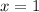 is local minimum.
is local minimum.
2)
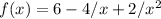
 and
and
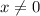
So the root is
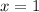
The function is increasing on the interval [1,∞)
The function is decreasing on the interval (-∞,0) ∪ (0,1]
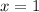 is absolute minimum.
is absolute minimum.
3)
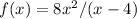
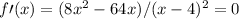 and
and

So the roots are
 and
and
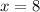
The function is increasing on the interval (-∞,0] ∪ [8,∞)
The function is decreasing on the interval [0,4) ∪ (4,8]
 is local maximum,
is local maximum,
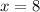 is local minimum.
is local minimum.
4)
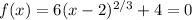
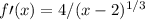 has no solution and
has no solution and
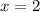 is crtitical point.
is crtitical point.
The function is increasing on the interval [2,∞)
The function is decreasing on the interval (-∞,2]
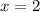 is absolute minimum.
is absolute minimum.
5)
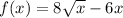 for
for
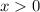

So the root is
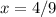
The function is increasing on the interval (0,4/9]
The function is decreasing on the interval [4/9,∞)
 is local minimum,
is local minimum,
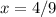 is absolute maximum.
is absolute maximum.