Question

when 6 is subtracted from the square of a number, the result is 5 times the number. Find the negative solution.

Answer 1

When 6 is subtracted from the square of a number, the result is 5 times the number, then the negative solution is -1

Solution:

Given that when 6 is subtracted from the square of a number, the result is 5 times the number

To find: negative solution

Let "a" be the unknown number

Let us analyse the given sentence

square of a number =
`a^2`

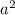
6 is subtracted from the square of a number =
`a^2 - 6`

5 times the number =
`5 * a`

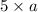
So we can frame a equation as:

6 is subtracted from the square of a number = 5 times the number

`a^2 - 6 = 5 * a\\\\a^2 -6 -5a = 0\\\\a^2 -5a -6 = 0`

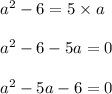
Let us solve the above quadratic equation

For a quadratic equation
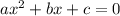`ax^2 + bx + c = 0` where
`a \\eq 0`

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

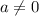
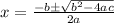
Here in this problem,

`a^2-5 a-6=0 \text { we have } a=1 \text { and } b=-5 \text { and } c=-6`

Substituting the values in above quadratic formula, we get

`\begin{array}{l}{a=\frac{-(-5) \pm \sqrt{(-5)^(2)-4(1)(-6)}}{2 * 1}} \\\\ {a=(5 \pm √(25+16))/(2)=(5 \pm √(49))/(2)} \\\\ {a=(5 \pm 7)/(2)}\end{array}`

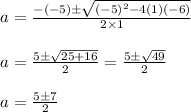
We have two solutions for "a"

`\begin{array}{l}{a=(5+7)/(2) \text { and } a=(5-7)/(2)} \\\\ {a=(12)/(2) \text { and } a=(-2)/(2)}\end{array}`

a = 6 or a = -1

We have asked negative solution. So a = -1

Thus the negative solution is -1