Question

A 425-kg satellite is launched into a circular orbit that has a period of 702 min and a radius of 20,100 km around Earth. (a) Determine the gravitational potential energy of the satellite’s orbit. (b) Estimate the energy required to place the satellite in orbit around Earth

Answer 1

a)
`-8.44 * 10^9` J

b)
`2.24 * 10^(10)` J

Step-by-step explanation:

Given and known parameters are:

Gravitational constant,
`G = 6.674*10^(-11)`
`N.(m/kg)^2`

Mass of Earth,
`M = 5.98 * 10^(24)` kg

Mass of satellite, m = 425 kg

Radius if Earth, R = 6370 km

Radius of satellite, r = 20100 km

Period, T = 702 min

a) Potential energy in the satellite's orbit is:

`PE = -(GMm)/(r) = -(6.674*10^(-11)*5.98 * 10^(24)*425)/(20100*10^3) = -8.44 * 10^9` J

b) To find the energy required to place the satellite in orbit around Earth, we need to determine kinetic energy KE and potential energy PE both initially at rest and finally in the orbit.

`PE_i =  -(GMm)/(R)\\KE_i = 0\\\\PE_f = -(GMm)/(r)\\KE_f = (GMm)/(2r)`

Hence,

`\Delta E = (KE + PE)_(final) - (KE+PE)_(initial) = (-(GMm)/(r)+-(GMm)/(2r)) - ((GMm)/(R))`

`= GMm((1)/(R)-(1)/(2r)) = 6.674*10^(-11)*5.98 * 10^(24)*425*((1)/(6.37*10^6)-(1)/(2*20.1*10^6))`

`= 2.24 * 10^(10)` J

Answer 2

a) U= -8.43 10 9 J b) 6.52 10⁹ J

Step-by-step explanation:

a) The potential energy can be determined from the relationship between force and energy

F = - dU / dr

dU = - F dr

We replace and integrate. If we take the positive direction in the direction of dr, the force goes in the opposite direction (attraction) therefore it is negative

F = - G mM / r²

∫ U = G mM ∫ dr / r²

U = G mM (- 1 / r)

We evaluate

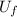`U_(f)` –U₀ = - G mM (1 /
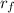`r_(f)` - 1 / r₀)

The reference system location is arbitrary, the most common choice is U₀ = 0 for r₀ = ∞

U = - G m M 1 / r

Let's reduce the magnitudes to the SI system

T = 702 min (60s / 1min) = 42120

R = 20100 km (1000m / 1km) = 2.01 10⁷ m

Let's calculate

U = -6.67 10⁻¹¹ 425 5.98 10²⁴ 1 / 2.01 10⁷

U= -8.43 10 9 J

b) The energy to place the satellite in orbit, This is equal to the mechanical energy of the system

Em = K + U

Em = ½ m v² +U

Since the satellite is in a circular orbit, the velocity module is constant

v = d / t

The distance of an orbit is the length of the circle and this time is called a period

d = 2π r

v = 2π r / T

We replace

Em = ½ m (2π r / T)² + U

Em = 2π² m r² / T² + U

Let's calculate

Em = 2π² 425 (2.01 10⁷)² / (4.2120 10⁴)² - 8.43 10⁹

Em = 1,910 10⁹ - 8.43 10⁹

Em = - 6.52 10⁹ J