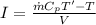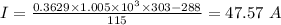Question

A 115-volt electrical heater is used to warm 0.3 m3/s of air at 100 kPa and 15°C to 100 kPa and 30°C. How much current in amperes must be supplied to this heater? The gas constant of air is 0.287 kPa·m3/kg·K. The constant pressure specific heat of air at room temperature is cp = 1.005 kJ/kg·°C.

Answer 1

The amount of current supplied to heater is 47.57 A

Solution:

As per the question:

Voltage of electric heater, V = 115 V

Volume rate of flow of air,
`\dot{V} = 0.3\ m^(3)/s`

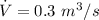
Initial temperature of air, T =
`15^(\circ)C` = 273 + 15 = 288 K

Final temperature of air, T' =
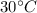`30^(\circ)C` = 273 + 30 = 303 K

Initial Pressure = Final Pressure, P = 100 kPa

Specific heat of air,
`C_(p) = 1.005\ kJ/kg.^(\circ)C`

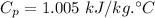
Gas constant, R = 0.287
`kPa.m^(3)/kg.K`

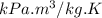
Now,

To compute the amount of current supplied to the heater, we assume the steady state operation and neglecting the effects of kinetic energy and potential energy:

Specific volume, 'v' of the air at the inlet is given by:

`v = (RT)/(P) = (0.287* 288)/(100)`

`v = 0.8266\ m^(3)/kg`

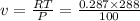
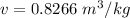
Mass flow rate of air can be given by:

`\dot{m} = \frac{\dot{V}}{\dot{v}}`

`\dot{m} = (0.3)/(0.8266) = 0.3629\ kg/s`

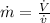
Considering the system of the pipe containing air and using the energy balance on this system:

`\Delta \dot{E} = \dot{E_(in)} - \dot{E_(out)}`

`\Delta \dot{E} = 0`

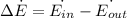
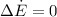
Therefore,

`\dot{E_(i)} = \dot{E_(out)}`

`\dot{E_(i)} = \dot{W} + \dot{m}h`

`\dot{E_(o)} = \dot{m}h'`

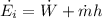
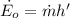
Thus

`\dot{W} = \dot{m}\Delta h`

Also, we know that:

`\dot{W} = V* I`

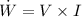
where

I = current in amperes

Now, comparing the two eqns, we get:

`I = \frac{\dot{m}C_(p){h' - h}}{V}`

`I = \frac{\dot{m}C_(p){T' - T}}{V}`

`I = \frac{0.3629* 1.005* 10^(3)* {303 - 288}}{115} = 47.57\ A`