Question

A Pew Internet poll asked cell phone owners about how they used their cell phones. One question asked whether or not during the past 30 days they had used their phone while in a store to call a friend or family member for advice about a purchase they were considering. The poll surveyed 1024 adults living in the United States by telephone. Of these, 471 responded that they had used their cell phone while in a store within the last 30 days to call a friend or family member for advice about a purchase they were considering. (a) Find (plusminus 0.0001) SE_p the sample proportion, the standard error of the sample proportion, and the margin of error for 95% confidence. p = SE_p = m = (b) Find the 95% large-sample confidence interval (plusminus 0.001) for the population proportion, the 95% large-sample confidence interval is from ____ to _____.

Answer 1

The student is asked to use the sample proportion from a survey to calculate the standard error, margin of error, and the 95% confidence interval for the population proportion. These statistics require formulas involving the sample proportion, the sample size, and the z-score for 95% confidence, followed by the addition and subtraction of the margin of error from the sample proportion.

Step-by-step explanation:

To answer the student's question regarding the sample proportion, the standard error (SEp), and the margin of error for a 95% confidence interval, we perform a series of calculations. The sample proportion (p) is found by dividing the number of adults who have used their cell phone in a store to call for advice about a purchase by the total number of adults surveyed, which is p = 471 / 1024.

To find the standard error of this proportion (SEp), we use the formula SEp = sqrt((p * (1 - p)) / n), where n is the sample size. Substituting our values, we get SEp = sqrt((471/1024) * (1 - (471/1024)) / 1024).

The margin of error (m) at 95% confidence can be calculated by multiplying the SEp by the z-score for a 95% confidence level, which is approximately 1.96. So, m = 1.96 * SEp.

To construct the 95% confidence interval, we add and subtract the margin of error from the sample proportion: lower limit = p - m, upper limit = p + m, rounding off to the nearest 0.001 as required.

Answer 2

a)
`\hat p=(471)/(1024)=0.460`

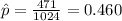
The standard error is given by:

`SE= \sqrt{(\hat p(1-\hat p))/(n)}=\sqrt{(0.460(1-0.460))/(1024)}=0.0156`

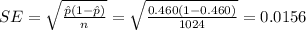
And the margin of error is given by:

`ME=z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}=1.96\sqrt{(0.460(1-0.460))/(1024)}=0.0305`

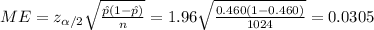
b) The 99% confidence interval would be given by (0.429;0.491)

Step-by-step explanation:

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The population proportion have the following distribution

`p \sim N(p,\sqrt{(p(1-p))/(n)})`

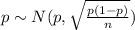
Data given and notation

n=1024 represent the random sample taken

X=471 represent the people responded that they had used their cell phone while in a store within the last 30 days to call a friend or family member for advice about a purchase they were considering

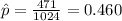`\hat p=(471)/(1024)=0.460` estimated proportion of people responded that they had used their cell phone while in a store within the last 30 days to call a friend or family member for advice about a purchase they were considering

p= population proportion of people responded that they had used their cell phone while in a store within the last 30 days to call a friend or family member for advice about a purchase they were considering

Part a

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

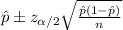
For the 95% confidence interval the value of
`\alpha=1-0.95=0.05` and
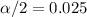`\alpha/2=0.025`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=1.96`

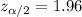
The standard error is given by:

`SE= \sqrt{(\hat p(1-\hat p))/(n)}=\sqrt{(0.460(1-0.460))/(1024)}=0.0156`

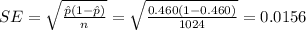
And the margin of error is given by:

`ME=z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}=1.96\sqrt{(0.460(1-0.460))/(1024)}=0.0305`

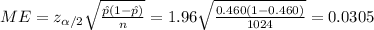
Part b

If we replace the values obtained we got:

`0.460-1.96\sqrt{(0.460(1-0.460))/(1024)}=0.429`

`0.460+1.96\sqrt{(0.460(1-0.460))/(1024)}=0.491`

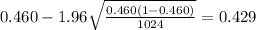
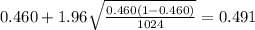
The 99% confidence interval would be given by (0.429;0.491)