Question

A student measures the maximum speed of a block undergoing simple harmonic oscillations of amplitude A on the end of a single ideal spring with spring constant k. The single spring is then replaced with 3 identical springs (in series) with the same spring constant k. If the same block undergoes SHM with the same amplitude before, by what factor does the maximum speed change?

Answer 1

Step-by-step explanation:

Given

Amplitude of oscillation is A

spring constant k

suppose m is the mass of block so its natural frequency of oscillation is given by

`\omega _n=\sqrt{(k)/(m)}`

`v_(max)=A\omega =A\cdot \sqrt{(k)/(m)}`

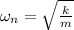
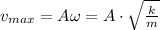
When three identical springs is connected in series

`k_(effectice)=(k)/(3)`

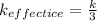
Natural Frequency becomes

`\omega _n=\sqrt{(k)/(3m)}`

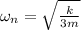
Thus maximum speed with Amplitude A is

`v'_(max)=A\cdot \sqrt{(k)/(3m)}`

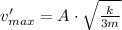
so by a factor of
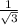`(1)/(√(3))` maximum velocity is changed