Question

A dumbbell-shaped object is composed by two equal masses,m, connected by a rod of negligible mass and lengthr. If "I1" is the moment of inertia of this object withrespect to an axis passing through the center of the rod andperpendicular to it and "I2" is the moment of inertia withrespect to an axis passing through one of the masses is I1 greaterthan, equal to, less than, or noncomparable to I2?

Answer 1

`I_1 = I_(left) + I_(right) = m(r/2)^2 + m(r/2)^2 = 2m(r^2/4) = (1)/(2)mr^2`

`I_2 = mr^2`

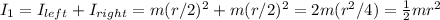
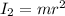
The moment of inertia of the object with respect to an axis passing through one of the masses is greater than the moment of inertia with respect to an axis passing through the center of the rod.

Hence,
`I_2 > I_1`

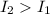
Step-by-step explanation:

Since the rod has negligible mass, it is straightforward to calculate the total moment of inertia of the object: the sum of moment of inertia of separate masses.

The moment of inertia of a point-like object is
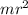`mr^2`, and their distance to the axis is
`r/2`.

In the second case,
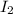`I_2`, The axis passes through one of the masses, so that mass does not have a contribution to the total moment of inertia of the object. The only contribution comes from the other mass, whose distance to the axis is
`r`.