Question

We wish to give a 90% confidence interval for the mean value of a normally distributed random variable. We obtain a simple random sample of 9 elements from the population on which the variable is defined. The sample has a mean value of 10.2 and a sample standard deviation 1.5. Find the 90% confidence interval for the mean value.

Answer 1

Answer:
`(9.27025,\ 11.12975)`

Explanation:

Given : Sample size : n= 9

Degree of freedom = df =n-1 =8

Sample mean :
`\overline{x}=10.2`

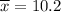
sample standard deviation :
`s= 1.5`

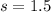
Significance level ;
`\alpha= 1-0.90=0.10`

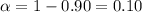
Since population standard deviation is not given , so we use t- test.

Using t-distribution table , we have

Critical value =
`t_(\alpha/2, df)=t_(0.05 , 8)=1.8595`

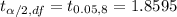
Confidence interval for the population mean :

`\overline{x}\pm t_(\alpha/2, df)(s)/(√(n))`

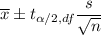
90% confidence interval for the mean value will be :

`10.2\pm (1.8595)(1.5)/(√(9))`

`10.2\pm (1.8595)(1.5)/(3)`

`10.2\pm (1.8595)(0.5)`

`10.2\pm (0.92975)`

`(10.2-0.92975,\ 10.2+0.92975)`

`(9.27025,\ 11.12975)`

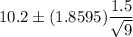
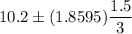
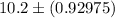
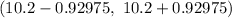
Hence, the 90% confidence interval for the mean value=
`(9.27025,\ 11.12975)`