Question

A commercial fishermen A, working alone, takes 4 hours longer to run the hoop nets than it takes fisherman B working alone. Together they can run the hoop nets in 5 5/6 hours. How long does it take each working alone?

Answer 1

A takes 14 hours and B takes 10 hours in working alone.

Explanation:

Let the time taken by B alone = x hours,

One hour work of B =
`(1)/(x)`

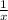
∵ fishermen A, working alone, takes 4 hours longer to run the hoop nets than it takes fisherman B working alone.

So, the time taken by A alone = (x+4) hours,

One hour work of A =
`(1)/(x+4)`

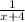
Thus, total one hour when A and B work simultaneously =
`(1)/(x)+(1)/(x+4)`

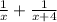
Since, together they take
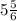`5(5)/(6)` hours

Total one hour work =
`(1)/(5(5)/(6))=(1)/((35)/(6))=(6)/(35)`

`\implies (1)/(x)+(1)/(x+4)=(6)/(35)`

`(x+4+x)/(x^2+4x)=(6)/(35)`

`(2x+4)/(x^2+4x)=(6)/(35)`

`70x + 140 = 6x^2 + 24x`

`6x^2 + 24x - 70x - 140=0`

`6x^2 - 46x - 140=0`

`3x^2 - 23x - 70=0`

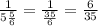
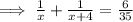
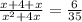
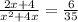
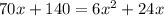
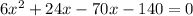
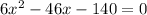
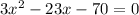
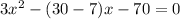`3x^2-(30-7)x - 70=0` ( Middle term splitting )

`3x^2 - 30x + 7x - 70=0`

`3x(x-10) + 7(x-10)=0`

`(3x+7)(x-10)=0`

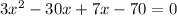
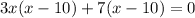
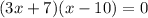
By zero product property,

3x + 7 = 0 or x - 10 =0

⇒ x = -7/3 ( not possible ) or x = 10

Hence, time taken by B = 10 hours,

Time taken by A = 10 + 4 = 14 hours