Answer:
A) 210
B) 357
C) 267
Explanation:
A) Among 7 games, we can first choose 3 wins, and then among remaining 4 games, we can choose 2.
To calculate the possibility, we will use Combination.
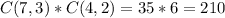
B) Player A can get 4 points with the following cases:
4 wins and 3 loses
3 wins, 2 draws and 2 loses
2 wins, 4 draws and 1 lose
1 win and 6 draws
Indeed, these cases matches for Player B too to get 3 points.
So again, we will use Combination to calculate the possibility.

C) Here, we need to find two possibilities after 6 games and add them, while Player A has 3 points and wins the 7th game, and Player A has 3.5 points and draws the 7th game.
![[C(6,3)+C(6,2)C(4,2)+C(6,1)C(5,4)+C(6,6)] + [C(6,3)C(3,1)+C(6,2)C(4,3)+C(6,1)] =[20+90+30+1]+[60+60+6]=141+126=267](https://img.qammunity.org/2020/formulas/mathematics/high-school/5gl4gr33lovlmdkvpj2x2es61gf7y6wvz4.png)