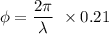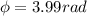Question

Two loudspeakers emit sound waves along the x-axis. A listener in front of both speakers hears a maximum sound intensity when speaker 2 is at the origin and speaker 1 is at x = 0.540 m . If speaker 1 is slowly moved forward, the sound intensity decreases and then increases, reaching another maximum when speaker 1 is at x = 0.870 m.

A) What is the phase difference between the speakers?
B) What is the frequency of the sound? Assume velocity of sound is 340m/s.

Answer 1

given,

difference between the two consecutive maximum

λ = 0.870 - 0.540

λ = 0.33 m

speed of sound = 340 m/s

b) frequency of the sound

v = f x λ

340 = f x 0.33

`f =(340)/(0.33)`

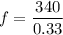
f = 1030.3 Hz

a) phase difference

the expression of phase difference is given by

`\phi = (2\pi)/(\lambda)\ \delta`

`\delta = \Delta x - \lambda`

`\delta = 0.540 - 0.33`

`\delta = 0.21\ m`

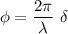
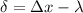
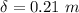
now,

`\phi = (2\pi)/(\lambda)\ * 0.21`

`\phi = (2\pi)/(0.33)\ * 0.21`

`\phi = 3.99 rad`