Question

A factory cans fresh pineapple in sugar syrup. The manager in charge is interested in estimating the average amount of sugar per can to within 2 mg of the true mean. From previous experiments, he knows that the (true) standard deviation of the sugar content is 15 mg. Each test of measuring the amount of sugar in a can costs $5.00. One thousand dollars have been budgeted for this experiment. Does the manager have enough funds to estimate the average amount of sugar per can with 95% confidence

Answer 1

No. He would need $1,080 to perform a test with this error.

Explanation:

To answer this question, we have to calculate the sample size. This is the sample size that allow to estimate the average amount of sugar per can with 95% confidence (95% CI).

The difference between the upper and lower limit of the CI have to be equal or less to e=2 mg. The z value for a 95% CI is z=1.96.

`e\leq z\sigma/√(n)`

`e=z\sigma/√(n)\\\\√(n)=z\sigma/e=\\\\n=(z\sigma/e)^2=(1.96*15/2)^2=14.7^2=216\\\\n=216`

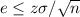
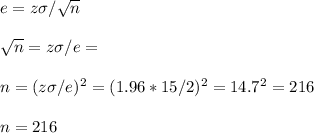
The minimum sample size needed for this error is 216. At a cost of $5/test, this sample size would cost
`n*p=216*5=\$ 1,080`.

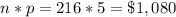This is over the budget for this experiment ($1000).