Question

A gas is said to be compressed adiabatically if there is no gain or loss of heat. When such a gas is diatomic (has two atoms per molecule), it satisfies the equation PV 1.4 = k, where k is a constant, P is the pressure, and V is the volume. At a given instant, the pressure is 23 kg/cm2, the volume is 35 cm3, and the volume is decreasing at the rate of 4 cm3/min. At what rate is the pressure changing?

Answer 1

The pressure is changing at
`(dP)/(dt)=3.68`

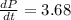
Explanation:

Suppose we have two quantities, which are connected to each other and both changing with time. A related rate problem is a problem in which we know the rate of change of one of the quantities and want to find the rate of change of the other quantity.

We know that the volume is decreasing at the rate of
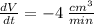`(dV)/(dt)=-4 \:{(cm^3)/(min)}` and we want to find at what rate is the pressure changing.

The equation that model this situation is

`PV^(1.4)=k`

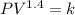
Differentiate both sides with respect to time t.

`(d)/(dt)(PV^(1.4))= (d)/(dt)k\\`

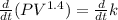
The Product rule tells us how to differentiate expressions that are the product of two other, more basic, expressions:

`\frac{d}{{dx}}\left( {f\left( x \right)g\left( x \right)} \right) = f\left( x \right)\frac{d}{{dx}}g\left( x \right) + \frac{d}{{dx}}f\left( x \right)g\left( x \right)`

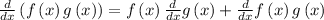
Apply this rule to our expression we get

`V^(1.4)\cdot (dP)/(dt)+1.4\cdot P \cdot V^(0.4) \cdot (dV)/(dt)=0`

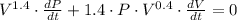
Solve for
`(dP)/(dt)`

`V^(1.4)\cdot (dP)/(dt)=-1.4\cdot P \cdot V^(0.4) \cdot (dV)/(dt)\\\\(dP)/(dt)=(-1.4\cdot P \cdot V^(0.4) \cdot (dV)/(dt))/(V^(1.4)) \\\\(dP)/(dt)=(-1.4\cdot P \cdot (dV)/(dt))/(V)}`

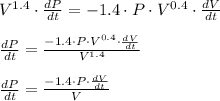
when P = 23 kg/cm2, V = 35 cm3, and
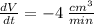`(dV)/(dt)=-4 \:{(cm^3)/(min)}` this becomes

`(dP)/(dt)=(-1.4\cdot P \cdot (dV)/(dt))/(V)}\\\\(dP)/(dt)=(-1.4\cdot 23 \cdot -4)/(35)}\\\\(dP)/(dt)=3.68`

The pressure is changing at
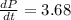`(dP)/(dt)=3.68`.