Answer:
9
Explanation:
The first simplification we can make is to replace 6^0 with 1.
The first rules of exponents we can apply are ...
(a·b)^c = a^c·b^c . . . . . . similar to the distributive property
(a^b)^c = a^(b·c)
This reduces your expression to ...
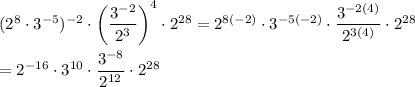
Now we can apply another two rules of exponents:
(a^b)(a^c) = a^(b+c)
1/a^b = a^-b
Using these, we have ...
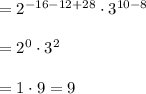
The value of the expression is 9.