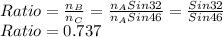Question

A layer of liquid B floats on liquid A. A ray of light begins in liquid A and undergoes total internal reflection at the interface between the liquids when the angle of incidence exceeds 32.0°. When liquid B is replaced with liquid C, total internal reflection occurs for angles of incidence greater than 46.0°. Find the ratio nB/nC of the refractive indices of liquids B and C.

Answer 1

0.737

Step-by-step explanation:

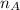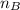`n_(A)` = Refractive indices of liquid A

`n_(B)` = Refractive indices of liquid B

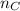`n_(C)` = Refractive indices of liquid C

Consider the total internal reflection at interface of liquid A and liquid B

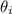`\theta_(i)` = Angle of incidence = 32.0

Using Snell's law for total internal reflection

`n_(A) Sin\theta_(i) = n_(B) \\n_(B) = n_(A) Sin32`

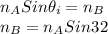
Consider the total internal reflection at interface of liquid A and liquid C

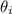`\theta_(i)` = Angle of incidence = 46

Using Snell's law for total internal reflection

`n_(A) Sin\theta_(i) = n_(C) \\n_(C) = n_(A) Sin46`

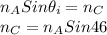
Ratio is hence given as

`Ratio = (n_(B))/(n_(C)) = (n_(A) Sin32)/(n_(A) Sin46) = (Sin32)/(Sin46)\\Ratio = 0.737`