The rate of change is
 and the initial value is 0.
and the initial value is 0.
To find the rate of change (slope) of the linear function from the graph, you can use the formula:
![\[ \text{Slope (m)} = \frac{\text{Change in y}}{\text{Change in x}} = (y_2 - y_1)/(x_2 - x_1) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/9rws8tg20472muqwj34gqb5qpthj16ehla.png)
From the graph, you need to select two points that the line passes through. Let's say we select the points (2, 1) and (7, 4).
Using these two points:
![\[ m = (4 - 1)/(7 - 2) = (3)/(5) \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/lc24zrvffyb6rpo66tk8djro7c4tjhvi1d.png)
So, the rate of change (slope) is
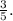
The initial value (y-intercept) is the value of y when x=0. Looking at the graph, the y-intercept appears to be at (0, 0).