Question

A large bell is hung from a wooden beam so it can swing back and forth with negligible friction. The center of mass of the bell is 0.80 m below the pivot, the bell has mass 30.0 kg , and the moment of inertia of the bell about an axis at the pivot is 15.0 kg⋅m2 . The clapper is a small, 1.8 kg mass attached to one end of a slender rod that has length L and negligible mass. The other end of the rod is attached to the inside of the bell so it can swing freely about the same axis as the bell. What should bethe length L of the clapper rod for the bell to ring silently, thatis, for the period of oscillation for the bell to equal that forthe clapper?

Answer 1

0.62499 m

Step-by-step explanation:

L = Length of the clapper rod

g = Acceleration due to gravity = 9.81 m/s²

I = Moment of inertia = 15 kgm²

m = Mass of bell = 30 kg

d = Distance to the bell = 0.8 m

Time period is given by

`T=2\pi\sqrt{(I)/(mgd)}\\\Rightarrow T=2\pi\sqrt{(15)/(30* 9.81* 0.8)}\\\Rightarrow T=1.58593\ s`

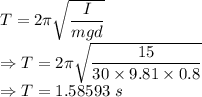
Time period of a simple pendulum is given by

`T_s=2\pi\sqrt{(L)/(g)}\\\Rightarrow L=g(T_s^2)/(4\pi^2)\\\Rightarrow L=9.81(1.58593^2)/(4\pi^2)\\\Rightarrow L=0.62499\ m`

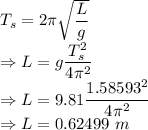
The time period of the pendulum and the simple pendulum is equal

The length of the clapper rod for the bell to ring silently is 0.62499 m