Question

A parachute jumper weighs 200 pounds (including gear), has a parachute with an area of 200 square feet, and a coefficient of drag of 1.0. What is the highest downward speed (the terminal velocity), in miles per hour, that this jumper can attain? At the terminal velocity the downward force (the weight) is equal to the upward force (the aerodynamic drag force).

Answer 1

To solve this problem it is necessary to apply the concepts related to the Drag Force and the Weight of a body described since Newton's second law.

The drag force is given as

`(1)/(2) \rho C_D v^2 A = W`

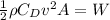
Where

`\rho`= Density

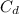`C_d`= Drag Coefficient

v = Velocity

A = Cross-sectional Area

W = Weight

Replacing to find the velocity we have that

`(1)/(2) \rho C_D v^2 A = W`

`(1)/(2) (2.38*10^(-3))(1)v^2 (200) = 200`

`V = 28.98ft/s`

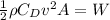
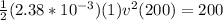
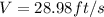
Converting these values to miles per hour we have to

`V = 28.98ft/s((3600s)/(1hour))((1mile)/(5280ft))`

`V = 19.76mi/h`

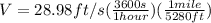
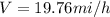
Therefore the highest downward speed that this jumper can attain is 19.76mi/h