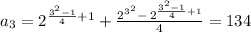Question

The nine squares of a 3-by-3 chessboard are to be colored red and blue. The chessboard is free to rotate but cannot be flipped over. Determine the generating function for the number of nonequivalent colorings and the total number of nonequivalent colorings.

Answer 1

`a_n = 2^{(n^2-1)/(4) + 1} + \frac{2^(n^2) - \, 2^{(n^2-1)/(4) + 1}}{4}`

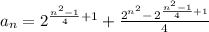
For n = 3, there are 134 possibilities

Explanation:

First, lets calculate the generating function.

For each square we have 2 possibilities: red and blue. The Possibilities between n² squares multiply one with each other, giving you a total of 2^n² possibilities to fill the chessboard with the colors blue or red.

However, rotations are to be considered, then we should divide the result by 4, because there are 4 ways to flip the chessboard (including not moving it), that means that each configuration is equivalent to three other ones, so we are counting each configuration 4 times, with the exception of configurations that doesnt change with rotations.

A chessboard that doesnt change with rotations should have, in each position different from the center, the same colors than the other three positions it could be rotated into. As a result, we can define a symmetric by rotations chessboard with only (n²-1)/4 + 1 squares (the quarter part of the total of squares excluding the center plus the center).

We cocnlude that the total of configurations of symmetrical boards is
`2^{(n^2-1)/(4) + 1}`

Since we have to divide by 4 the rest of configurations (because we are counted 4 times each one considering rotations), then the total number of configutations is

`a_n = 2^{(n^2-1)/(4) + 1} + \frac{2^(n^2) - \, 2^{(n^2-1)/(4) + 1}}{4}`

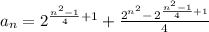
If n = 3, then the total amount of possibilities are

`a_3 = 2^{(3^2-1)/(4) + 1} + \frac{2^(3^2) - \, 2^{(3^2-1)/(4) + 1}}{4} =  134`