Answer: $35 is the selling price and $1225 is the maximum revenue.
Explanation:
Since we have given that
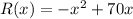
We need to find the maximum revenue.
So, We will first derivative it w.r.t. x.
So, it becomes,

Now, we will find critical points.
So, R'(x) = 0
So, it becomes,
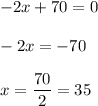
Now, to check whether it yields maximum revenue or not.
So, second derivative w.r.t. x, we get that
R''(x) = -2<0
So, At $35, it yields maximum revenue.
Amount of maximum revenue would be
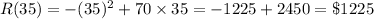
Hence, $35 is the selling price and $1225 is the maximum revenue.