Question

A random sample of the correct choice on 400 multiple-choice questions on a variety of AP exams1 shows that B was the most common correct choice, with 90 of the 400 questions having B as the answer. Does this provide evidence that B is more likely to be the correct choice than would be expected if all five options were equally likely? Show all details of the test. The data are available in APMultipleChoice.

a) State the null and alternative hypotheses

b) Calculate the test statistic and p-value

Answer 1

a) Null hypothesis:
`p\leq 0.2`

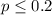
Alternative hypothesis:
`p > 0.2`

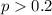
b)
`z=\frac{0.225 -0.2}{\sqrt{(0.2(1-0.2))/(400)}}=1.25`

`p_v =P(Z>1.25)=0.106`

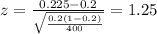
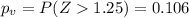
Explanation:

1) Data given and notation

n=400 represent the random sample taken

X=90 represent the number of questions with B as the correct answer

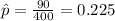`\hat p=(90)/(400)=0.225` estimated proportion of arrests that were not prosecuted

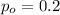`p_o=0.2` is the value that we want to test, since we assume that each question present 5 options and just one is correct, 1/5 =0.2 if all five options were equally likely

`\alpha` represent the significance level

z would represent the statistic (variable of interest)

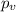`p_v` represent the p value (variable of interest)

2) Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that the true proportion is higher than 0.2.:

Null hypothesis:
`p\leq 0.2`

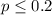
Alternative hypothesis:
`p > 0.2`

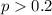
When we conduct a proportion test we need to use the z statisitc, and the is given by:

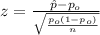`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
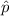`\hat p` is significantly different from a hypothesized value
`p_o`.

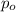3) Calculate the statistic

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.225 -0.2}{\sqrt{(0.2(1-0.2))/(400)}}=1.25`

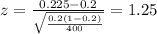
4) Statistical decision

It's important to refresh the p value method or p value approach . "This method is about determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.

The significance level provided
`\alpha`. The next step would be calculate the p value for this test.

Since is a right tailed test the p value would be:

`p_v =P(Z>1.25)=0.106`

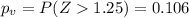
If we compare the p value obtained and the significance level assumed
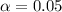`\alpha=0.05` we have
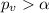`p_v>\alpha` so we can conclude that we have enough evidence to FAIL reject the null hypothesis, and we can said that at 5% of significance the proportion of B correct answers is not significantly higher than 0.2.