Question

A 57 kg skier starts from rest at a height of H = 27 m above the end of the ski-jump ramp. As the skier leaves the ramp, his velocity makes an angle of 28° with the horizontal. Neglect the effects of air resistance and assume the ramp is frictionless.

(a) What is the maximum height h of his jump above the end of the ramp?
(b) If he increased his weight by putting on a backpack, would h then be greater, less or, the same?

Answer 1

(a)
`h=5.95m`

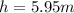
(b) h is the same

Step-by-step explanation:

According to the law of conservation of energy:

`E_i=E_f\\U_i+K_i=U_f+K_f`

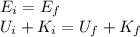
The skier starts from rest, so
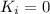`K_i=0` and we choose the zero point of potential energy in the end of the ramp, so
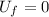`U_f=0`. We calculate the final speed, that is, the speed when the skier leaves the ramp:

`mgH=(mv^2)/(2)\\v=√(2gH)\\v=\sqrt{2(9.8(m)/(s^2))(27m)}\\v=23(m)/(s)`

Finally, we calculate the maximum height h above the end of the ramp:

`v_f^2=v_i^2-2gh\\`

The initial vertical speed is given by:

`v_i=vsin\theta`

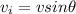
and the final speed is zero, solving for h:

`h=(v_i^2)/(2g)\\h=(((23(m)/(s))sin(28^\circ))^2)/(2(9.8(m)/(s^2)))\\h=5.95m`

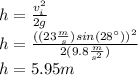
(b) We can observe that the height reached does not depend on the mass of the skier