Answer: a. 0.8
Explanation:
When we test whether the variances of the two populations are equal we use F- test.
Test statistic :
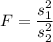
, where
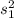 = sample variance from population 1.
= sample variance from population 1.
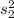 = sample variance from population 2.
= sample variance from population 2.
As per given , we have
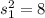 and
and
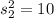
Then, If we test whether the variances of the two populations are equal, the test statistic will be
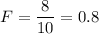
Hence, the test statistic will have a value of 0.8 .
Thus , the correct answer is a. 0.8 .