Question

Which point is the solution to the following system of equations?

x² + y² = 13
2x- y=4
(-2, -3)
(-3, -2)
(2,3)
(3, 2)​

Answer 1

The point (3, 2) is the solution to given system of equations

Solution:

Given that system of equations are:

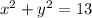`x^2 + y^2 = 13` ------ eqn 1

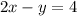`2x - y = 4` ------- eqn 2

From eqn 2,

y = 2x - 4

Substitute y = 2x - 4 in eqn 1

`x^2 + (2x - 4)^2 = 13\\\\x^2 + 4x^2 + 16 - 16x = 13\\\\5x^2 -16x + 3 = 0`

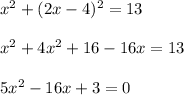
Let us solve the above equation by quadratic formula,

`\text {For a quadratic equation } a x^(2)+b x+c=0, \text { where } a \\eq 0\\\\x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`

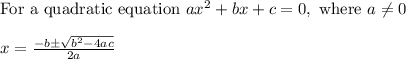
Using the Quadratic Formula for
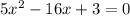`5x^2 -16x + 3 = 0` where a = 5, b = -16, and c = 3

`\begin{aligned}&x=\frac{-(-16) \pm \sqrt{(-16)^(2)-4(5)(3)}}{2 * 5}\\\\&x=(16 \pm √(256-60))/(10)\\\\&x=(16 \pm √(196))/(10)\end{aligned}`

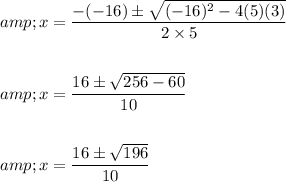
The discriminant
`b^2 - 4ac>0` so, there are two real roots.

`\begin{aligned}&x=(16 \pm √(196))/(10)=(16 \pm 14)/(10)\\\\&x=(16+14)/(10) \text { or } (16-14)/(10)\\\\&x=(30)/(10) \text { or } x=(2)/(10)\\\\&x=3 \text { or } x=0.2\end{aligned}`

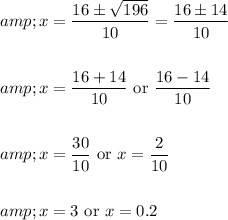
Substitute for x = 0.2 and x = 3 in 2x - y = 4

when x = 3

2(3) - y = 4

6 - y = 4

y = 2

when x = 0.2

2(0.2) - y = 4

0.4 - y = 4

y = 0.4 - 4

y = -3.6

Thus Option D is correct The point is (3, 2)