Whats linear and non linear? y=22−5x y=x3 y=x3+13

Question

asked Sep 1, 2020 4.5k views

1 Answer

Ambertch · Answer 1 · 2020-09-07T17:55:19+0000

Answer:

Linear :

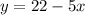
Non linear :
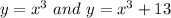
$y=x^3\ and\ y=x^3+13$

Explanation:

Given:

The equations given are:

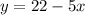
y=22-5x

y=x^3

y=x^3+13

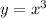
Now, a linear equation is of the form:

y=mx+b

Where, 'm' and 'b' are real numbers and 'm' not equal to 0.

The highest exponent of 'x' in a linear equation is always 'one'.

Therefore, if the exponent of 'x' in an equation is anything other than 'one', then the equation is a nonlinear equation.

The equation
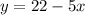y=22-5x can be rewritten as:

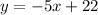
y=-5x+22

The above equation is of the form of a linear equation with
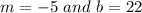$m=-5\ and\ b=22$ . So, this represents a linear equation.

The other two equations have exponent 3 for 'x' which is not '1'. So, these equations are nonlinear equations.