Question

Sean wants to spend (example) $100 on clothing and he wants to purchase

6 additional items for his wardrobe. Each pair of pants costs $20 and each
shirt costs $15.

a. What is the system of equations that represents this situation?

b. Can he buy 2 pair of pants and 4 shirts?

Answer 1

a) 20x+15y=100

b) Yes, Sean can purchase 2 pairs of pants and 4 shirts

Explanation:

Hope this helps

Answer 2

a) The system of equation representing the situation is
`20x+15y\leq 100`

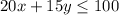
b) Sean can buy 2 pair of pants and 4 shirts with the money he needs to spend.

Explanation:

Given:

Total money need to spend on clothing = $100

Cost of each pair of pant = $20

Cost of each shirt = $15

Let the number pair of pants be 'x'.

Let number of shirts be 'y'.

Solving for part a.

We need to find the system of equation representing the situation.

Now we know that Total Money spent is less than or equal to sum of Cost of each pant multiplied by number of pair of pants and Cost of each shirt multiplied by number of shirts.

Framing in equation form we get;

`20x+15y\leq 100`

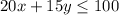
Hence, The system of equation representing the situation is
`20x+15y\leq 100`

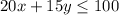
Now Solving for part b.

We need to find whether he can buy 2 pairs of pants and 4 shirts.

Which means
`x=2;y=4\\`

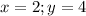
Substituting the values we get;

`20x+15y\leq 100\\\\20*2+15*4\leq 100\\\\40+60\leq 100\\\\100\leq 100`

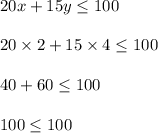
Since the amount required to buy 2 pants and 4 shirts is equal to amount of money he has.

Hence Sean can buy 2 pair of pants and 4 shirts with the money he needs to spend.