Question

The position of an object at time t is given by s(t) = 6 - 14t. Find the instantaneous velocity at t = 6 by finding the derivative.

By using the difference quotient

Answer 1

It results -14 in either way

Explanation:

Velocity As A Rate Of Change

The velocity of an object can be computed as the rate of change of its displacement (or position taken as a vector) over time. If we compute it as a derivative, it's called instantaneous velocity, and if computed as the slope of the function (difference quotient) at a certain point it's the average velocity

The position of the object as a function of time is

`\displaystyle s(t)=6-14t`

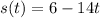
Computing the derivative

`\displaystyle s'(t)=-14`

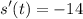
We can see it's a constant value. If we use the slope or rate of change:

`\displaystyle v=(s_2-s_1)/(t_2-t_1)`

Now let's fix two values for time

`\displaystyle t_1=5\ sec,\ t_2=8\ sec`

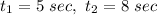
and compute the corresponding positions, by using the given function

`\displaystyle s_1=6-14(5)=-64`

`\displaystyle s_2=6-14(8)=-106`

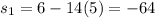
Now we compute the average velocity

`\displaystyle v=(-106-(-64))/(8-5)`

`\displaystyle v=(-106+64)/(3)=(-42)/(3)`

`\displaystyle v=-14`

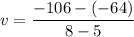
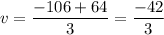
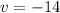
We get the very same result in both ways to compute v. It happens because the position is related with time as a linear function, it's called a constant velocity motion.