Question

company manufactures and sells x cellphones per week. The weekly​ price-demand and cost equations are given below. p equals 500 minus 0.5 xp=500−0.5x and Upper C (x )equals 25 comma 000 plus 140 xC(x)=25,000+140x ​(A) What price should the company charge for the​ phones, and how many phones should be produced to maximize the weekly​ revenue

Answer 1

The number of cellphones to be produced per week is 500.

The cost of each cell phone is $250.

The maximum revenue is $1,25,000

Explanation:

We are given the following information in the question:

The weekly​ price-demand equation:

`p(x)=500-0.5x`

The cost equation:

`C(x) = 25000+140x`

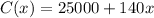
The revenue equation can be written as:

`R(x) = p(x)* x\\= (500-0.5x)x\\= 500x - 0.5x^2`

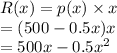
To find the maximum value of revenue, we first differentiate the revenue function:

`\displaystyle(dR(x))/(dx) = (d)/(dx)(500x - 0.5x^2) = 500-x`

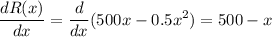
Equating the first derivative to zero,

`\displaystyle(dR(x))/(dx) = 0\\\\500-x = 0\\x = 500`

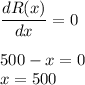
Again differentiating the revenue function:

`\displaystyle(dR^2(x))/(dx^2) = (d)/(dx)(500 - x) = -1`

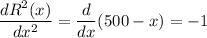
At x = 500,

`\displaystyle(dR^2(x))/(dx^2) < 0`

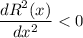
Thus, by double derivative test, R(x) has the maximum value at x = 500.

So, the number of cellphones to be produced per week is 500, in order to maximize the revenue.

Price of phone:

`p(500)=500-0.5(500) = 250`

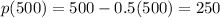
The cost of each cell phone is $250.

Maximum Revenue =

`R(500) = 500(500) - 0.5(500)^2 = 125000`

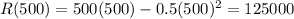
Thus, the maximum revenue is $1,25,000