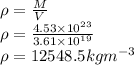Question

An artificial satellite is in a circular orbit above the surface of a planet of radius the period of revolution of the satellite around the planet is . What is the average density of the planet?

Answer 1

`12548.5 kgm^(-3)`

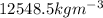
Step-by-step explanation:

Complete statement of the question is

An artificial satellite is in a circular orbit d = 310 km above the surface of a planet of radius r = 2050 km. The period of revolution of the satellite around the planet is T = 1.15 hours. What is the average density of the planet?

`r` = radius of the planet = 2050 km = 2.05 x 10⁶ m

`d` = distance of the satellite above the surface of planet = 310 km = 0.310 x 10⁶ m

`R` = radius of the orbit =
`r + d` =
`2.05*10^(6) + 0.31*10^(6) = 2.36*10^(6) m`

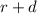`M` = mass of the planet

`T` = Time period of the planet = 1.15 h = 1.15 x 3600 = 4140 s

Using Kepler's third law

`T^(2) = (4\pi^(2) R^(3) )/(GM) \\4140^(2) = (4(3.14)^(2) (2.36*10^(6))^(3) )/((6.67*10^(-11))M)\\M = 4.53*10^(23) kg`

Volume of the planet is given as

`V = (4\pi r^(3) )/(3) \\V = (4(3.14) (2.05*10^(6))^(3) )/(3)\\V = 3.61*10^(19) m^(3)`

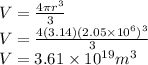
Average density of the planet is given as

`\rho = (M)/(V) \\\rho = (4.53*10^(23))/(3.61*10^(19))\\\rho = 12548.5 kgm^(-3)`