Question

A physics exam consists of 9 multiple-choice questions and 6 open-ended problems in which all work must be shown. If an examinee must answer 7 of the multiple-choice questions and 3 of the open-ended problems, in how many ways can the questions and problems be chosen?

Answer 1

720 ways

Explanation:

Generally, combination is expressed as;

`^(n) C_(r) = (n!)/(r!(n-r)!)`

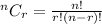
The question consists of 9 multiple-choice questions and examinee must answer 7 of the multiple-choice questions.

⇒ ⁹C₇
`=(9!)/(7!(9-7)!)`

`=(9!)/(7!(2)!)`

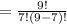
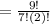
= 36

The question consists of 6 open-ended problems and examinee must answer 3 of the open-ended problems.

⇒ ⁶C₃
`=(6!)/(3!(6-3)!)`

`=(6!)/(3!(3)!)`

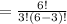
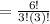
= 20

Combining the two combinations to determine the number of ways the questions and problems be chosen if an examinee must answer 7 of the multiple-choice questions and 3 of the open-ended problem.

⁹C₇ × ⁶C₃

= 36 × 20

= 720 ways