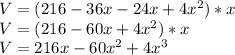Question

An artist cuts 4 squares with sides of length x ft from the corners of a 12 ft-by-18 ft rectangular piece of sheet metal. She bends up the sides and welds the corners to form a rectangular garden fountain that is x ft high. Write and simplify a function for the volume V of the fountain in terms of x

Answer 1

`V = 216x - 60x^2 + 4x^3`

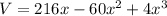
Explanation:

The volume V of the fountain is equal to:

V = L*W*h

Where L is the lenght of the fountain, W is the width of the fountain and h is the high of the fountain

We already know that h is equal to x. On the other hand, if we cut a square with side of length x, L and W are calculated as:

L = 18 - 2x

W = 12 - 2x

So, replacing L, W and h on the equation of the volume, we get:

V = (18-2x)*(12-2x)*x

Finally, simplifying the function we get:

`V = ((18*12)+(18*(-2x))+(-2x*12)+((-2x)*(-2x)))*x`

`V = (216-36x-24x+4x^2)*x\\V = (216-60x+4x^2)*x\\V = 216x - 60x^2 + 4x^3`