Answer:
J=36221 Kg.m/s
Step-by-step explanation:
Impulse-Momentum Theorem
These two magnitudes are related in the following way. Suppose an object is moving at a certain speed
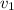 and changes it to
and changes it to
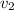 . The impulse is numerically equivalent to the change of linear momentum. Let's recall the momentum is given by
. The impulse is numerically equivalent to the change of linear momentum. Let's recall the momentum is given by
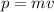
The initial and final momentums are, respectively
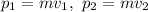
The change of momentum is
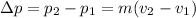
It is numerically equal to the Impulse J
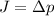
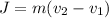
We are given
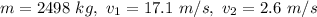
The impulse the car experiences during that time is
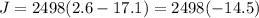
J=-36221 Kg.m/s
The magnitude of J is
J=36221 Kg.m/s