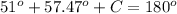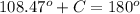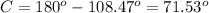Question

Solve the following triangle. Given A=51 degrees b=40 c=45

Answer 1

`a=36.87\ units`

`B=57.47^o`

`C=71.53^o`

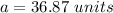
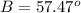
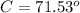
Explanation:

step 1

Find the length side a

Applying the law of cosines

`a^2=b^2+c^2-2(b)(c)cos(A)`

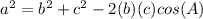
substitute the given values

`a^2=40^2+45^2-2(40)(45)cos(51^o)`

`a^2=1,359.4466`

`a=36.87\ units`

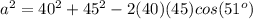
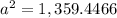
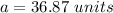
step 2

Find the measure of angle B

Applying the law of sines

`(a)/(sin(A)) =(b)/(sin(B))`

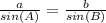
substitute the given values

`(36.87)/(sin(51^o)) =(40)/(sin(B))`

`sin(B)=(sin(51^o))/(36.87){40}`

`B=sin^(-1)((sin(51^o))/(36.87){40})=57.47^o`

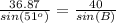
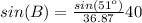
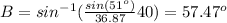
step 3

Find the measure of angle C

Remember that the sum of the interior angles in any triangle must be equal to 180 degrees

so

`A+B+C=180^o`

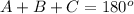
substitute the given values

`51^o+57.47^o+C=180^o`

`108.47^o+C=180^o`

`C=180^o-108.47^o=71.53^o`