Question

At 1:00pm, ship A is 30 miles due south of ship B and is sailing north at a rate of 15 mi/hr. If ship B is sailing

west at a rate of 10 mi/hr, find the time at which the distance d between the ships is minimal.

Answer 1

2:23 pm

Explanation:

We can solve this considering a a right triangle

let t = travel time of both ships

therefore,

15t = distance traveled by ship A

however, it is traveling toward the point of reference, therefore we write it

(30-15t)

and

10t = distance traveled by ship B, away from the point of reference

Let d = distance between the ships at t time, (the hypotenuse of the right triangle)

`d= √((30-15t)^2+10t^2)`

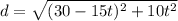
and combine like terms

`d= √((900-900t+225t^2)+100t^2)`

`d= √(3325t^2-900t+900)`

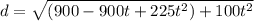
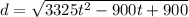
from this d to minimum we can find the axis of symmetry, where in

a=325 and b= -900

the t=-b/2a

`t= -(-900)/(2*325)`

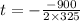
t= 1.384 hours

now putting the value we get

`d= √(3325(1.384)^2-900(1.384)+900)`

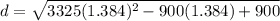
solving this we get

d= 16.64 miles

therefore,

16.64 mi apart after 1.3846 hrs, minimum distance between the ships

now, 1.384 hours = 1+60(0.348) hour

= 1 hour and 23 minutes

so, the time at which the distance d between the ships is minimal = 1:00 pm + 1 hour and 23 minutes = 2:23 pm