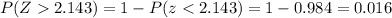Question

Student scores on exams given by a certain instructor have mean 74 and standard deviation 14. This instructor is about to give two exams, one to a class of size 25 and the other to a class of size 64. Approximate the probability that the average test score in the class of size 25 exceeds 80.

Answer 1

`P(\bar X >80)=P(Z>2.143)=1-P(z<2.143)=1-0.984=0.016`

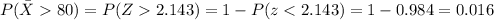
Explanation:

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

Let X the random variable that represent the Student scores on exams given by a certain instructor, we know that X have the following distribution:

`X \sim N(\mu=74, \sigma=14)`

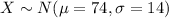
The sampling distribution for the sample mean is given by:

`\bar X \sim N(\mu,(\sigma)/(√(n)))`

The deduction is explained below we have this:

`E(\bar X)= E(\sum_(i=1)^(n)(x_i)/(n))= \sum_(i=1)^n (E(x_i))/(n)= (n\mu)/(n)=\mu`

`Var(\bar X)=Var(\sum_(i=1)^(n)(x_i)/(n))= (1)/(n^2)\sum_(i=1)^n Var(x_i)`

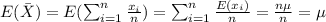
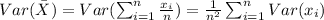
Since the variance for each individual observation is
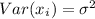`Var(x_i)=\sigma^2` then:

`Var(\bar X)=(n \sigma^2)/(n^2)=(\sigma)/(n)`

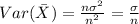
And then for this special case:

`\bar X \sim N(74,(14)/(√(25))=2.8)`

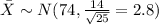
We are interested on this probability:

`P(\bar X >80)`

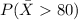
And we have already found the probability distribution for the sample mean on part a. So on this case we can use the z score formula given by:

`z=(\bar X -\mu)/((\sigma)/(√(n)))`

Applying this we have the following result:

`P(\bar X >80)=P(Z>(80-74)/((14)/(√(25))))=P(Z>2.143)`

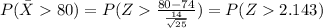
And using the normal standard distribution, Excel or a calculator we find this:

`P(Z>2.143)=1-P(z<2.143)=1-0.984=0.016`