Question

At the beginning of an environmental study a forest cover an area of 1500 km second power since then this area has decreased by 9.8% each year let T be the number of years since the start of the study letter y b the area that the forest covers in km to the second power write an exponential function showing the relationship between Y&T

Answer 1

`y=1500\cdot(0.902)^T`

Explanation:

Let T be the number of years since the start of the study and y be the area that the forest covers in
`\text{km}^2`.

We have been given that at the beginning of an environmental study a forest cover an area of 1500
`\text{km}^2`. Since then this area has decreased by 9.8% each year.

We know that an exponential function is in form
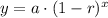`y=a\cdot(1-r)^x`, where,

y = Final amount,

a = Initial amount,

r = Decay rate in decimal form,

x = Time.

Let us convert 9.8% into decimal as:

`9.8\%=(9.8)/(100)=0.098`

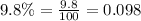
We have been given that initial value (a) is
`1500`.

Upon substituting our given values, we will get:

`y=1500\cdot(1-0.098)^T`

`y=1500\cdot(0.902)^T`

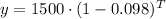
Therefore, our required exponential function would be
`y=1500\cdot(0.902)^T`.