Answer:
if r=4:
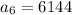
if r=1/4:

Explanation:
Geometric and Arithmetic Progressions
We define a geometric progression when each term
 is defined as the previous term
is defined as the previous term
 times a constant called the common ratio. The iterative formula is
times a constant called the common ratio. The iterative formula is
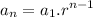
In an arithmetic progression, each term is found by adding a constant called common difference, to the previous term
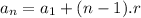
We are given the condition that the sum of the three first terms of a geometric progression is 126
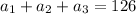
Using the iterative formula, we have
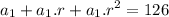
Taking a common factor
![\displaystyle a_1(1+r+r^2)=126....[eq\ 1]](https://img.qammunity.org/2020/formulas/mathematics/high-school/efg7tvvim7buc3kh3pkmlaggvhpfngickm.png)
We also know that if 14, 36, and 4 are added to each term, respectively, the new numbers form an arithmetic progression. It means they will have a common difference. The new numbers will be
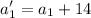
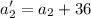
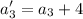
The common difference between term 2 and term 1 is

Using the iterative formula again
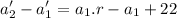
The common difference between term 3 and term 2 is
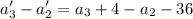
Using the iterative formula again
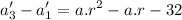
Both common differences must be equal
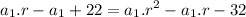
Rearranging
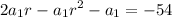
Solving for

![\displaystyle a_1=(54)/(1-2r+r^2)......[eq\ 2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/g9cdj69olkxqqcq4megnrmbrb5i42vm0og.png)
Replacing in eq 1
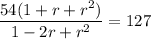
Dividing by 18 and cross-multiplying
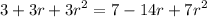
Rearranging we have a second-degree equation
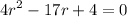
Factoring
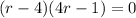
The solutions are
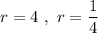
If r=4, and using eq 2
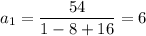
Having
 and r, we compute
and r, we compute
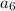
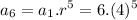
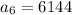
If we use the other solution r=1/4
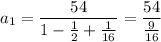
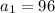
The sixth term is
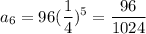

Both solutions are feasible