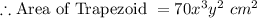Question

What is the area of a trapezoid with height 14xy^2 cm, a base with length 3x^2 cm, and another base length 7x^2 cm?

Answer 1

`\therefore \textrm{Area of Trapezoid }= 70x^(3)y^(2)\ cm^(2)`

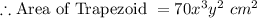
Explanation:

Given:

Shape is of Trapezoid

Height = 14xy² cm

Length 1 = 3x² cm ( one Parallel side)

Length 2 = 7x² cm ( other Parallel side)

To Find:

Area of Trapezoid = ?

Solution:

We know that

`\textrm{Area of Trapezoid }= 0.5(length\ 1+length\ 2)Height`

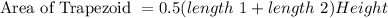
substituting the given values we get

`\textrm{Area of Trapezoid }= 0.5*(3x^(2)+7x^(2))* 14xy^(2)`

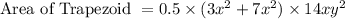
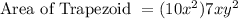`\textrm{Area of Trapezoid }= (10x^(2))7xy^(2)`..((x^{a}x^{b}=x^{(a+b)})

`\therefore \textrm{Area of Trapezoid }= 70x^(3)y^(2)\ cm^(2)`