Answer:
Increasing in x < 7 and decreasing in x > 7.
Explanation:
g(x) = 1 -
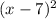
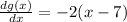
If a function is increasing in a interval, its first derivative is positive and if a function is decreasing in an intreval, its first derivative is negative.
Using this concept here,
Substitute x > 7,
the first derivative is negative.Hence it is decreasing in this interval.
Substitute x < 7,
The first derivative is positive.Hence it is increasing in this interval.
Hence the answer is increasing in x < 7 and decreasing in x > 7.