Question

Lisa has \dfrac{1}{3} 3 1 ​ start fraction, 1, divided by, 3, end fraction of an hour to read and watch television. She wants to split her time equally between the two activities.

Answer 1

Lisa spends
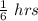`(1)/(6)\ hrs` in reading and
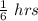`(1)/(6)\ hrs` in watching television.

Explanation:

Given:

Number of hours Lisa has =
`(1)/(3)`

Now we need to find number of hours required to watch television and to read.

Given:

She splits her time equally between 2 activities.

Hence we can say;

Number of hours required to watch television and number of hours required to read both are half times equal to total number of hours.

Hence framing the equation we get;

Number of hours required to watch television =
`(1)/(2) * \textrm{Total Number of hours she has}`

Substituting the value we get;

Number of hours required to watch television =
`(1)/(2) * (1)/(3) = (1)/(6)\ hrs`

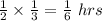
Number of hours required to read =
`(1)/(2) * \textrm{Total Number of hours she has}`

Substituting the values we get;

Number of hours required to read =
`(1)/(2) * (1)/(3) = (1)/(6)\ hrs`

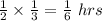
Hence Lisa spends
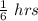`(1)/(6)\ hrs` in reading and
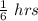`(1)/(6)\ hrs` in watching television.