Answer:
A) reflection across the y-axis
Explanation:
If
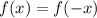 , then this says that two
, then this says that two
 -coordinates are equal for opposite values of
-coordinates are equal for opposite values of
 .
.
Let
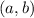 a point on
a point on
 .
.
Then
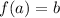 .
.
We also know that
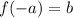 and therefore
and therefore
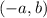 is also a point on the graph.
is also a point on the graph.
If you graph [/tex](-a,b)[/tex] and
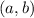 you will see they are symmetrical to each about the
you will see they are symmetrical to each about the
 -axis.
-axis.
Example if given both
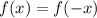 and
and
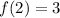 , then
, then
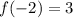 . This means both (2,3) and (-2,3) are points on the graph.
. This means both (2,3) and (-2,3) are points on the graph.
Here is what those two points look like on a Cartesian Plane (please see graph in picture).