Question

13 pigs are entered in the "Best Pig" competition at the county fair. The judges

will award very special pigs with blue, red, and white ribbons. In how many
different ways can these ribbons be awarded to 3 of the 13 pigs?

Answer 1

The answer is 3 because their are only 3 ribbons

Answer 2

There are 286 different ways to award the blue, red, and white ribbons to 3 out of the 13 pigs.

Using the concept of combinations.

The formula for combinations is given by:

`\[ C(n, r) = (n!)/(r!(n-r)!) \]`

In this case, we want to find
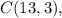`\(C(13, 3)\),` which represents the number of ways to choose 3 pigs out of 13 for the ribbons.

`\[ C(13, 3) = (13!)/(3!(13-3)!) \]`

Calculate the factorials and simplify the expression to find the answer:

`\[ C(13, 3) = (13!)/(3! * 10!) \]`

`\[ C(13, 3) = (13 * 12 * 11)/(3 * 2 * 1) \]`

`\[ C(13, 3) = (1716)/(6) \]`

`\[ C(13, 3) = 286 \]`

Therefore, there are 286 different ways to award the blue, red, and white ribbons to 3 out of the 13 pigs.