Answer:
Diameter of pound = 10 yd
Explanation:
Given area of circular pond = 78.5 square yd
To find the diameter of the pond.
Solution:
The pond being circular in shape, the area of pond can be given as:
⇒
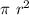
where
 represents radius of the pond.
represents radius of the pond.
Thus, we have:
⇒
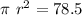
Using
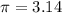
⇒
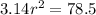
Solving for

Dividing both sides by 3.14
⇒
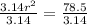
⇒
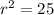
Taking square root both sides.
⇒
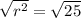
⇒
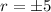
So, radius = 5 yd, as distances are always positive.
Diameter =
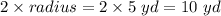
Thus, diameter of pound = 10 yd