Question

Triangle PQR with vertices P(3, −6), Q(6, −9), and R(−15, 3) is dilated by a scale factor of 3 to obtain triangle P′Q′R′. Which statement best describes triangle P′Q′R′?A. It is similar to triangle PQR and has coordinates P′(1, −2), Q′(2, −3), and R′(−5, 1).B. It is congruent to triangle PQR and has coordinates P′(1, −2), Q′(2, −3), and R′(−5, 1).C. It is similar to triangle PQR and has coordinates P′(9, −18), Q′(18, −27), and R′(−45, 9).D. It is congruent to triangle PQR and has coordinates P′(9, −18), Q′(18, −27), and R′(−45, 9).

Answer 1

C

Explanation:

Answer 2

Option C.

Explanation:

The vertices of triangle PQR are P(3, −6), Q(6, −9), and R(−15, 3).

It is given that triangle PQR dilated by a scale factor of 3 to obtain triangle P′Q′R′.

We know that a figure and its image after dilation are similar. It means triangle PQR and triangle P′Q′R′

If a figure dilated by factor k about the origin then

`(x,y)\rightarrow (kx,ky)`

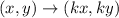
PQR dilated by a scale factor of 3, so

`(x,y)\rightarrow (3x,3y)`

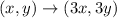
Using this rule we get

`P(3,-6)\rightarrow P'(3(3),3(-6))=P'(9,-18)`

`Q(6,-9)\rightarrow Q'(3(6),3(-9))=Q'(18,-27)`

`R(-15,3)\rightarrow R'(3(-15),3(3))=R'(-45,9)`

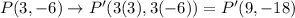
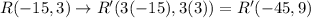
The vertices of image are P'(9,-18), Q'(18,-27) and R'(-45,9).

Therefore, the correct option is C.