Question

Consult Conceptual Example 9 in preparation for this problem. Interactive LearningWare 6.3 also provides useful background. The drawing shows a person who, starting from rest at the top of a cliff, swings down at the end of a rope, releases it, and falls into the water below. There are two paths by which the person can enter the water. Suppose he enters the water at a speed of 13.4 m/s via path 1. How fast is he moving on path 2 when he releases the rope at a height of 2.34 m above the water? Ignore the effects of air resistance.

Answer 1

11.56066 m/s

Step-by-step explanation:

m = Mass of person

v = Velocity of person = 13.4 m/s

g = Acceleration due to gravity = 9.81 m/s²

v' = Velocity of the person in the second

The kinetic and potential energy will balance each other at the surface

`(1)/(2)mv^2=mgh\\\Rightarrow h=(v^2)/(2g)\\\Rightarrow h=(13.4^2)/(2* 9.81)\\\Rightarrow h=9.15188\ m`

Height of the cliff is 9.15188 m

Let height of the fall be h' = 2.34 m

`(1)/(2)mv'^2+mgh'=mgh\\\Rightarrow v'=√(2g(h-h'))\\\Rightarrow v'=√(2* 9.81(9.15188-2.34))\\\Rightarrow v'=11.56066\ m/s`

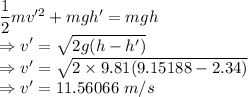
The speed of the person is 11.56066 m/s