Question

The length of a swimming pool is 3 feet longer than it's width. The swimming pool is surrounded by a deck that is 2 feet wide and has an area of 116 square feet. Find the dimensions of the pool

Answer 1

The Dimension of the pool is approximately 5.37 feet and 8.37 feet.

Explanation:

Given:

Area of Swimming Pool = 116 sq. ft

The length of a swimming pool is 3 feet longer than it's width.

Let the width of swimming pool be 'x' feet.

∴Length =
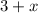`3+x` feet

Also given :

The swimming pool is surrounded by a deck that is 2 feet wide.

Hence we can say the deck is surrounded 2 feet on all 4 sides.

hence;

Length of swimming pool will become =
`3+x+4 = 7+x`

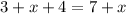
Width of swimming pool will become =
`x+4`

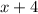
Since Swimming pool is in rectangular shape.

Now we know that area of Swimming pool is equal to length multiplied by width.

Framing in equation form we get;

`\textrm{Area of Swimming Pool}= length * width`

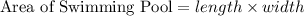
Substituting the given values we get;

`(x+7)(x+4)=116`

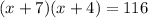
Solving the equation we get;

`x^2+4x+7x+28=116\\\\x^2+11x+28-116=0\\\\x^2+11x- 88 = 0`

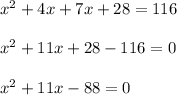
Now solving this equation by using quadratic formula we get;

According to the Quadratic Formula, x , the solution for
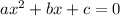`ax^2+bx+c  = 0` , where a, b and c are numbers, often called coefficients, is given by :

`x = (-b\±√(b^2-4ac))/(2a)`

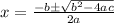
in our case a = 1 , b = 11 and c = -88

`b^2-4ac = 11^2-4* 1* -88 = 121+352 = 473`

`x= \frac{-11\±√(473)} {2*1}`

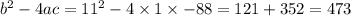
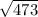`√(473)`, rounded to 4 decimal digits, is 21.7486.

`x=(-11\±21.7486)/(2)`

Two real solutions:

`x=(-11+21.7486)/(2) = 5.374\ ft`

OR

`x=(-11-21.7486)/(2) = -16.374\ ft`

Since width of the swimming pool cannot be negative value

hence we will consider
`x=5.374`

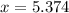
Rounding to nearest hundred we get;

Width of Swimming pool = 5.37 feet

Length of Swimming pool = 3+5.37 =8.37 feet

Hence The Dimension of the pool is approximately 5.37 feet and 8.37 feet.