Question

A 1500-kg car starts from rest at the top of a driveway 6.61 m long that is sloped at an angle of 20 degrees with the horizontal. If an average friction force of 3340 N impedes the motion of the car, find the speed (in m/s) of the car at the bottom of the driveway.

Answer 1

7.77114 m/s

Step-by-step explanation:

m = Mass of the car = 1500 kg

g = Acceleration due to gravity = 9.81 m/s²

h = Height of the driveway = 6.61 m

`\theta` = Angle = 30°

f = Frictional force = 3340 N

The potential energy will balance the kinetic energy of the car

`mghsin\theta-f=(1)/(2)mv^2\\\Rightarrow v=\sqrt{(2(mghsin\theta-f))/(m)}\\\Rightarrow v=\sqrt{(2(1500* 9.81* 6.61* sin30-3340))/(1500)}\\\Rightarrow v=7.77114\ m/s`

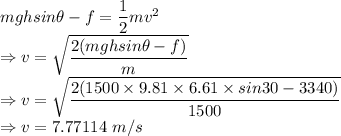
The speed of the car at the bottom of the driveway is 7.77114 m/s