Question

How is the factoring method GROUPING different from the factoring method GCF?

Answer 1

Explanation:

The basic concept for both is the same, except with grouping you have more than 3 terms and after factoring out what is common in each group, you are left with identical terms in a set of parenthesis that can then also be factored out. For example, this would be factoring by grouping (then I will show you a factoring by GCF to better illustrate the idea):

If our polynomial is

`x^3-x^2+3x-3=0`

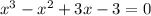
we could group those terms into groups of 2 (without changing their order at all) to get:

`(x^3-x^2)+(3x-3)=0`

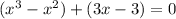
and we factor out what's common in each group to get:

`x^2(x-1)+3(x-1)=0`

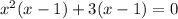
You can see that the (x - 1) is common now and can be factored out, leaving us with

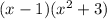`(x-1)(x^2+3)` (the secod term now can be factored if you need the complete linear factorization, but it will lead to imaginary numbers).

An example of factoring out the GCF is to factor out what's common in all the terms. It HAS TO BE COMMON IN ALL THE TERMS to do it this way. For example, in the polynomial

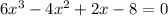`6x^3-4x^2+2x-8=0` the GCF for all the terms is a 2, so that's all we can factor out. It has to factor out of every term every time, no exceptions:

`2(3x^3-2x^2+x-4)=0`

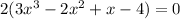
The method of GCF factoring often just serves to simplify the polynomial down a bit, but sometimes will still require factoring.