Answer:
a) 95.4% of the men are between 169cm and 193cm
b) 68.2% of the men are between 175cm and 187cm
Explanation:
The empirical rule, also known as three-sigma rule or 68-95-99.7 rule, "is a statistical rule which states that for a normal distribution, almost all data falls within three standard deviations (denoted by σ) of the mean (denoted by µ)".
Let X the random variable who represent the Heights of men on a baseball team.
From the problem we have the mean and the standard deviation for the random variable X.

So we can assume

On this case in order to check if the random variable X follows a normal distribution we can use the empirical rule that states the following:
• The probability of obtain values within one deviation from the mean is 0.68 2
• The probability of obtain values within two deviation's from the mean is 0.95 4
• The probability of obtain values within three deviation's from the mean is 0.997
a. 169cm and 193cm
We can find the deviations from the mean using the z score formula given by:
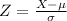
IF we find the z score for 169 and 193 we got:
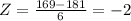
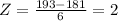
Since we are within 2 deviations from the mean and using the empirical rule we have 95.4% of the data
95.4% of the men are between 169cm and 193cm
b. 175cm and 187cm
We can find the deviations from the mean using the z score formula given by:
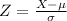
IF we find the z score for 169 and 193 we got:
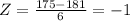
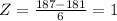
Since we are within 1 deviations from the mean and using the empirical rule we have 68.2% of the data
68.2% of the men are between 175cm and 187cm