Question

Solve for x in the equation x2 - 14x+31 = 63-

0
x= -16 or x = 2
x=-7+3.17
x=-2 or x = 16
x= 7+3/7
0
0

Answer 1

Solve for x in the equation x^2 - 14x + 31 = 63?

Answer:

The value of x for given equation is x = 16 or x = -2

Solution:

Given that equation is
`x^2 - 14x + 31 = 63`

To find: value of "x"

Subtract 63 from both sides we have:

`x^2 - 14x + 31 -63 = 63 - 63\\\\x^2 - 14x - 32 = 0`

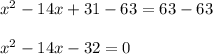
Now we will factor our given quadratic equation by splitting the middle term.

-14x can be splitted as -16x + 2x

`x^2 -16x + 2x - 32 = 0`

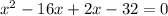
Take "x" as common from first two terms and "2" as common from last two terms

`x(x-16)+2(x-16)=0`

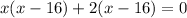
Take (x-16) common we have:

`(x - 16)(x + 2) = 0`

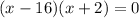
Equating the terms to 0,

x - 16 = 0 or x + 2 = 0

x = 16 or x = -2

Therefore, the value of x are: 16 and -2